Đạo hàm là một trong những khái niệm cốt lõi nhất trong giải tích, đóng vai trò quan trọng trong việc nghiên cứu tốc độ thay đổi của các hàm số. Cho dù bạn là học sinh THPT đang chuẩn bị cho kỳ thi hay sinh viên đại học muốn củng cố kiến thức, việc nắm vững các công thức đạo hàm sẽ giúp bạn giải quyết hiệu quả nhiều bài toán phức tạp.
Trong bài viết này, Westlink sẽ trình bày một cách toàn diện và chi tiết nhất tất cả các công thức đạo hàm cơ bản, kèm theo những ví dụ minh họa cụ thể để bạn có thể áp dụng ngay vào thực tế.

1. Bảng công thức đạo hàm cơ bản
Để làm chủ đạo hàm, việc đầu tiên bạn cần làm là nắm vững các công thức đạo hàm cơ bản. Đây chính là “viên gạch” đầu tiên để xây dựng những phép tính phức tạp hơn.
1.1 Đạo hàm của các hàm số sơ cấp
Các hàm số sơ cấp là nền tảng của mọi phép tính đạo hàm. Dưới đây là những công thức thường xuất hiện trong các bài toán cơ bản.mà bạn cần ghi nhớ:

1.2 Đạo hàm của các hàm cấp cao
Trong một số trường hợp, bạn sẽ gặp các hàm số phức tạp hơn, có thể được coi là sự kết hợp của nhiều hàm số cơ bản.

1.3 Đạo hàm của các hàm lượng giác
Các hàm lượng giác xuất hiện thường xuyên trong toán học và vật lý, do đó việc thuộc lòng các công thức này rất quan trọng:

1.4 Đạo hàm của biến số, hàm số và phân thức hữu tỉ
Đây là những trường hợp phức tạp hơn mà bạn sẽ gặp trong các bài toán thực tế:

2. Quy tắc tính đạo hàm
Bên cạnh các công thức cơ bản, bạn cần nắm vững các quy tắc tính đạo hàm để có thể xử lý các hàm số phức tạp hơn, được tạo thành từ tổng, hiệu, tích hoặc thương của nhiều hàm số khác.
Quy tắc chung: Giả sử u=u(x) và v=v(x) là các hàm số có đạo hàm trên một khoảng nào đó.
- Đạo hàm của tổng và hiệu:
- (u±v)′=u′±v′
- Giải thích: Đạo hàm của một tổng (hoặc hiệu) bằng tổng (hoặc hiệu) các đạo hàm.

- Đạo hàm của tích:
- (u⋅v)′=u′⋅v+u⋅v′
- Giải thích: Đạo hàm của một tích bằng đạo hàm của hàm thứ nhất nhân với hàm thứ hai, cộng với hàm thứ nhất nhân với đạo hàm của hàm thứ hai.
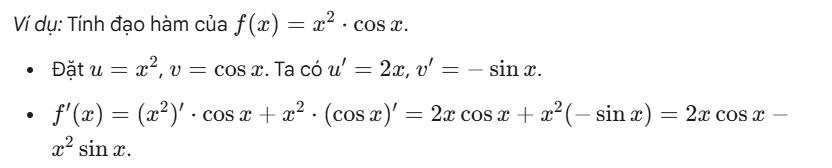
- Đạo hàm của thương:
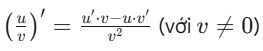
-
- Giải thích: Đạo hàm của một thương bằng đạo hàm của tử số nhân mẫu số, trừ đi tử số nhân đạo hàm của mẫu số, tất cả chia cho bình phương của mẫu số.
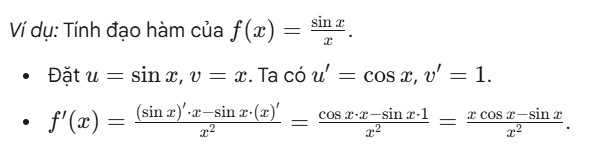
3. Các bài tập và ví dụ liên quan
Lý thuyết là quan trọng, nhưng thực hành mới giúp bạn nắm vững kiến thức. Dưới đây là một số bài tập và ví dụ minh họa để bạn áp dụng các công thức và quy tắc đã học.
Bài Tập Cơ Bản
Bài 1: Tính đạo hàm của các hàm số sau: a) f(x) = 3x⁴ – 2x³ + 5x – 1 b) g(x) = √x + 1/x² c) h(x) = e^x · ln x
Lời giải: a) f'(x) = 12x³ – 6x² + 5 b) g'(x) = 1/(2√x) – 2/x³ c) h'(x) = e^x · ln x + e^x · (1/x) = e^x(ln x + 1/x)
Bài Tập Nâng Cao
Bài 2: Tính đạo hàm của y = (x² + 1)²·sin(2x)
Lời giải: Đây là tích của hai hàm, ta áp dụng quy tắc tích:
u = (x² + 1)², u’ = 2(x² + 1)·2x = 4x(x² + 1)
v = sin(2x), v’ = 2cos(2x)
y’ = 4x(x² + 1)·sin(2x) + (x² + 1)²·2cos(2x)
y’ = 2(x² + 1)[2x sin(2x) + (x² + 1)cos(2x)]
Bài 3: Tính đạo hàm của y = ln(cos x)/tan x
Lời giải: Đây là thương của hai hàm:
u = ln(cos x), u’ = -sin x/cos x = -tan x
v = tan x, v’ = sec²x
y’ = (-tan x·tan x – ln(cos x)·sec²x)/(tan x)²
y’ = (-tan²x – ln(cos x)·sec²x)/tan²x
Bài Tập Thực Tế
Bài 4: Một vật chuyển động theo phương trình s(t) = t³ – 6t² + 9t + 2 (s tính bằng mét, t tính bằng giây). Tìm vận tốc và gia tốc của vật tại thời điểm t = 2 giây.
Lời giải:
Vận tốc: v(t) = s'(t) = 3t² – 12t + 9
Tại t = 2: v(2) = 3(4) – 12(2) + 9 = 12 – 24 + 9 = -3 m/s
Gia tốc: a(t) = v'(t) = s”(t) = 6t – 12
Tại t = 2: a(2) = 6(2) – 12 = 0 m/s²
Hy vọng rằng bài viết này đã cung cấp cho bạn một cái nhìn tổng quan và chi tiết nhất về công thức đạo hàm, từ những công thức cơ bản đến các quy tắc tính đạo hàm phức tạp hơn. Việc nắm vững các công thức này không chỉ giúp bạn giải quyết tốt các bài toán trong học tập mà còn là nền tảng vững chắc cho việc tiếp thu các kiến thức toán học cao hơn, cũng như ứng dụng vào các lĩnh vực thực tế.
Hãy luyện tập thường xuyên với các ví dụ và bài tập khác nhau để củng cố kiến thức và nâng cao kỹ năng tính toán của mình. Chúc bạn học tập tốt và áp dụng thành công các công thức đạo hàm vào thực tế!


