Hình vuông là một trong những hình học cơ bản, xuất hiện phổ biến trong toán học và đời sống hàng ngày. Việc nắm vững cách tính chu vi hình vuông không chỉ giúp bạn dễ dàng giải các bài toán mà còn áp dụng công thức trong thực tế. Bài viết dưới đây giúp bạn khám phá chi tiết công thức tính chu vi của hình vuông, cách áp dụng qua các bài tập minh họa, những lỗi sai cần tránh và ứng dụng thực tiễn của chu vi hình vuông.

1. Định nghĩa hình vuông
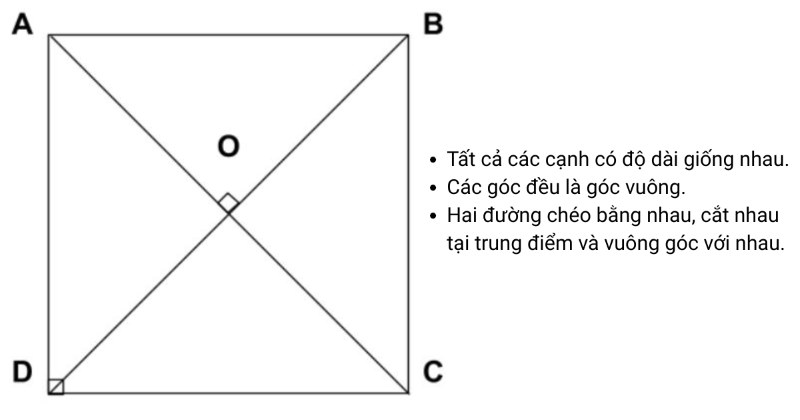
Hình vuông là một hình tứ giác đặc biệt có bốn cạnh bằng nhau và bốn góc vuông (mỗi góc bằng 90 độ). Đây là một dạng của hình chữ nhật, trong đó chiều dài và chiều rộng bằng nhau. Hình vuông có các đặc điểm nổi bật như:
- Tất cả các cạnh có độ dài giống nhau.
- Các góc đều là góc vuông.
- Hai đường chéo bằng nhau, cắt nhau tại trung điểm và vuông góc với nhau.
2. Chu vi hình vuông là gì?
Chu vi hình vuông là tổng độ dài của bốn cạnh của hình. Vì hình vuông có bốn cạnh bằng nhau, việc tính chu vi trở nên rất đơn giản. Chu vi thường được ký hiệu là P (Perimeter) và được đo bằng đơn vị độ dài như mét (m), centimet (cm), hoặc milimet (mm).
3. Công thức tính chu vi của hình vuông
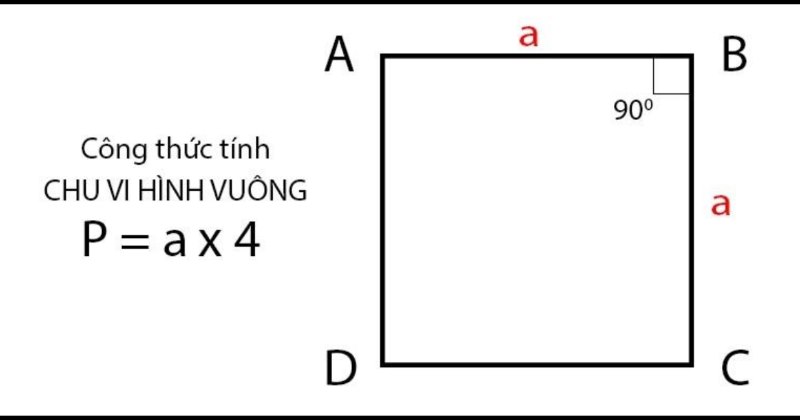
Công thức tính chu vi của hình vuông rất dễ nhớ:
P = 4 × a
Trong đó:
P: Chu vi của hình vuông
a: Độ dài một cạnh của hình vuông.
Ví dụ: Nếu một hình vuông có cạnh dài 5cm, chu vi sẽ là:
P = 4 × 5 = 20 cm.
4. Cách tính chu vi hình vuông qua bài tập minh họa cụ thể
Công thức tính chu vi hình vuông không quá phức tạp để những bạn học sinh ghi nhớ. Nắm được một số dạng bài tập liên quan sẽ giúp các bạn nhỏ hiểu và vận dụng tốt công thức này.
4.1. Tính chu vi của hình vuông khi biết độ dài cạnh
Bài toán: Một hình vuông có độ dài cạnh là 8 cm. Hãy tính chu vi của hình vuông.
Hướng dẫn giải:
Áp dụng công thức: P = 4 × a.
Chu vi hình vuông là: P = 4 × 8 = 32cm.
4.2. Tìm cạnh hình vuông khi biết chu vi
Bài toán: Một hình vuông có chu vi là 24 cm. Hãy tìm độ dài cạnh của hình vuông.
Hướng dẫn giải:
Công thức: P = 4 × a → a = P ÷ 4.
Độ dài cạnh của hình vuông là: a = 24 ÷ 4 = 6 cm.
4.3. Tính chu vi khi diện tích được biết
Bài toán: Một hình vuông có diện tích là 16 cm². Hãy tính chu vi của hình vuông.
Hướng dẫn giải:
Công thức diện tích hình vuông: S = a².
Tìm cạnh: a = √S = √25 = 5 cm.
Chu vi của hình vuông: P = 4 × a = 4 ×5 = 20cm.
5. Những lưu ý và lỗi sai thường gặp khi tính chu vi hình vuông
Mặc dù cách tính chu vi hình vuông khá đơn giản, nhưng trong quá trình học tập và làm bài tập, nhiều học sinh vẫn thường mắc phải những lỗi cơ bản.
5.1. Nhầm lẫn giữa chu vi và diện tích
Nhầm lẫn giữa chu vi và diện tích là lỗi phổ biến nhất, đặc biệt ở học sinh tiểu học khi bạn nhỏ chưa hiểu rõ định nghĩa và hình dung cụ thể hai khái niệm trên. Chu vi là tổng độ dài các cạnh bao quanh hình vuông, trong khi diện tích lại là phần không gian nằm bên trong hình.
- Chu vi có đơn vị là độ dài: cm, m, km,…
- Diện tích có đơn vị là diện tích: cm², m², km²,…
Mỗi khi tiếp nhận bài toán liên quan đến hình vuông, hãy đọc cẩn thận và xác định rõ đề bài yêu cầu chu vi hay diện tích trước khi áp dụng công thức.
5.2. Quên nhân với 4
Một lỗi phổ biến nữa khi tính chu vi hình vuông là chỉ ghi độ dài một cạnh mà quên nhân với 4. Do hình vuông có 4 cạnh bằng nhau, nên khi tính chu vi, nhất định phải nhân độ dài một cạnh với 4.
5.3. Dùng sai đơn vị đo
Việc không đồng nhất đơn vị trước khi tính toán sẽ dẫn đến kết quả sai. Từ đó dẫn đến kết quả không cao dù bạn có nhớ công thức chu vi hình vuông chính xác.
Ví dụ:
Cạnh hình vuông: 5m
Tính chu vi hình vuông theo đơn vị tính cm.
Ta có: P = 4 x a
P = 4 x 5 = 20m = 2000cm
Với lỗi sai cơ bản này, hãy luôn quy đổi về cùng một đơn vị đo trước khi tính toán và ghi kết quả kèm đơn vị chính xác.
5.4. Nhầm lẫn công thức với các hình khác
Trong quá trình làm bài, vì có nhiều công thức đối với mỗi dạng hình học khác nhau, nhiều bạn sẽ thường nhầm lẫn với công thức tính khác.
Ví dụ:
Công thức tính chu vi hình vuông: P = 4 x a
Công thức tính chu vi hình chữ nhật: P = (a + b) x 2
Trước khi làm toán, hãy luôn xác định rõ hình dạng trước khi chọn công thức.
6. Ứng dụng thực tế của chu vi hình vuông
Hiểu và vận dụng cách tính chu vi hình vuông không chỉ giúp học tốt môn Toán mà còn rất hữu ích trong nhiều tình huống thực tế.
6.1. Trong xây dựng và kiến trúc
Trong ngành xây dựng và kiến trúc, công thức tính chu vi hình vuông được sử dụng để xác định lượng vật liệu cần thiết cho các cấu trúc hoặc bề mặt có hình dạng hình vuông. Một số ứng dụng cụ thể bao gồm:

- Xây dựng tường hoặc hàng rào: Khi xây dựng một bức tường hoặc hàng rào bao quanh một khu đất hình vuông, chu vi giúp xác định chiều dài tổng cộng của vật liệu cần dùng, như gạch, bê tông, hoặc dây thép.
Ví dụ: Một khu vườn hình vuông có cạnh 10m cần làm hàng rào. Chu vi là P = 4 × 10 = 40m. Như vậy, cần 40m dây thép hoặc gỗ để làm hàng rào.
- Lát gạch sàn hoặc tường: Trong các công trình lát gạch cho sàn nhà hoặc tường hình vuông, chu vi giúp tính toán số lượng gạch viền hoặc vật liệu trang trí cần thiết.
Ví dụ: Một căn phòng hình vuông có cạnh 5m cần lát gạch viền quanh mép sàn. Chu vi là P = 4 × 5 = 20m, tức là cần 20m gạch viền.
- Thiết kế cửa sổ hoặc khung cửa: Các cửa sổ hoặc khung cửa hình vuông yêu cầu tính chu vi để xác định chiều dài khung kim loại hoặc gỗ.
Ví dụ: Một cửa sổ hình vuông có cạnh 1,2m cần khung nhôm. Chu vi là P = 4 × 1,2 = 4,8m, tức là cần 4,8m nhôm để làm khung.
Những ứng dụng này cho thấy công thức tính chu vi của hình vuông giúp tiết kiệm chi phí và tối ưu hóa vật liệu trong xây dựng.
6.2. Trong thiết kế nội thất và trang trí
Trong lĩnh vực thiết kế nội thất, công thức chu vi hình vuông đóng vai trò quan trọng trong việc lập kế hoạch và thực hiện các dự án trang trí. Một số ứng dụng cụ thể:
- May rèm hoặc vải bọc: Khi làm rèm cửa hoặc bọc ghế hình vuông, chu vi giúp xác định lượng vải cần thiết.
Ví dụ: Một bàn ăn hình vuông có cạnh 1,5 m cần may khăn trải bàn với viền trang trí. Chu vi là P = 4 × 1,5 = 6 m, tức là cần ít nhất 6 m vải viền.
- Làm khung tranh hoặc gương: Các khung tranh hoặc gương hình vuông yêu cầu tính chu vi để xác định chiều dài vật liệu làm khung, như gỗ, nhựa, hoặc kim loại.
Ví dụ: Một bức tranh hình vuông có cạnh 0,8 m cần làm khung gỗ. Chu vi là P = 4 × 0,8 = 3,2 m, tức là cần 3,2 m gỗ.
- Bố trí đồ nội thất: Khi thiết kế không gian, chu vi hình vuông giúp xác định cách sắp xếp đồ đạc hoặc tính toán không gian viền xung quanh một khu vực hình vuông.
Ví dụ: Một tấm thảm hình vuông có cạnh 2 m cần đặt trong phòng khách. Chu vi là P = 4 × 2 = 8 m, giúp xác định khoảng không gian viền xung quanh thảm để bố trí sofa hoặc bàn.

Những ứng dụng này cho thấy công thức chu vi hình vuông giúp các nhà thiết kế nội thất lập kế hoạch chính xác, tiết kiệm vật liệu và tạo ra không gian thẩm mỹ.
6.3. Trong nông nghiệp và quy hoạch đất đai
Trong nông nghiệp và quy hoạch đất đai, công thức đơn giản trên được sử dụng để quản lý và phân chia tài nguyên hiệu quả. Một số ứng dụng cụ thể:
- Làm hàng rào cho khu đất: Các khu đất nông nghiệp hoặc vườn cây hình vuông cần hàng rào để bảo vệ. Chu vi giúp xác định chiều dài hàng rào cần thiết.
Ví dụ: Một mảnh đất hình vuông có cạnh 50m cần làm hàng rào lưới. Chu vi là P = 4 × 50 = 200m, tức là cần 200m lưới thép.
- Phân chia đất đai: Khi chia đất thành các ô hình vuông để trồng trọt hoặc chăn nuôi, chu vi giúp xác định ranh giới và tính toán vật liệu cho các hàng rào phân chia.
Ví dụ: Một trang trại chia đất thành các ô hình vuông có cạnh 20 m. Mỗi ô có chu vi P = 4 × 20 = 80m, giúp tính tổng chiều dài dây thép cần cho tất cả các ô.

- Hệ thống tưới tiêu: Trong các hệ thống tưới tiêu cho cánh đồng hình vuông, chu vi giúp xác định chiều dài ống dẫn nước hoặc rãnh tưới bao quanh khu vực.
Ví dụ: Một cánh đồng hình vuông có cạnh 30 m cần lắp ống tưới xung quanh. Chu vi là P = 4 × 30 = 120m, tức là cần 120m ống dẫn.
Những ứng dụng này minh họa cách công thức tính chu vi của hình vuông hỗ trợ nông dân và kỹ sư nông nghiệp quản lý tài nguyên hiệu quả.
6.4. Trong giáo dục và đào tạo
Trong lĩnh vực giáo dục, chu vi hình vuông là một khái niệm cơ bản giúp học sinh xây dựng nền tảng toán học và tư duy logic. Các ứng dụng cụ thể bao gồm:
- Dạy học hình học: Giáo viên sử dụng công thức chu vi hình vuông để giới thiệu các khái niệm về chu vi, hình học phẳng, và mối quan hệ giữa các đại lượng (như chu vi và diện tích).
Ví dụ: Học sinh được yêu cầu tính chu vi hình vuông có cạnh 4cm (P = 4 × 4 = 16cm) để hiểu cách áp dụng công thức.
- Bài tập thực hành thực tế: Các bài toán về chu vi hình vuông thường được thiết kế để liên hệ với đời sống, giúp học sinh thấy được giá trị thực tiễn của toán học.
Ví dụ: Một bài toán yêu cầu học sinh tính chu vi khu vườn hình vuông để làm hàng rào, giúp các em áp dụng kiến thức vào tình huống thực tế.
- Phát triển tư duy không gian: Việc tính chu vi hình vuông giúp học sinh hình dung về không gian, kích thước, và cách đo lường, từ đó phát triển kỹ năng tư duy hình học.
Ví dụ: Học sinh vẽ một hình vuông và tính chu vi để hiểu mối quan hệ giữa các cạnh và tổng chu vi.
Những ứng dụng này cho thấy công thức chu vi hình vuông là công cụ quan trọng trong việc giảng dạy và học tập, giúp học sinh không chỉ nắm vững lý thuyết mà còn biết cách áp dụng vào thực tế.
6.5. Trong các lĩnh vực khác
Ngoài các lĩnh vực trên, cách tính chu vi hình vuông còn được ứng dụng trong nhiều ngành nghề và tình huống khác:
- Sản xuất công nghiệp: Trong sản xuất, chu vi hình vuông được dùng để tính toán vật liệu cho các sản phẩm có hình dạng vuông, như hộp kim loại, tấm bảng, hoặc linh kiện điện tử.
Ví dụ: Một nhà máy sản xuất tấm kim loại hình vuông có cạnh 0,5m. Chu vi P = 4 × 0,5 = 2m giúp xác định lượng vật liệu viền cần thiết.
- Thiết kế đồ họa và nghệ thuật: Các nhà thiết kế sử dụng chu vi hình vuông để tạo khung hoặc viền cho các tác phẩm nghệ thuật, logo, hoặc giao diện website.
Ví dụ: Một logo hình vuông có cạnh 10cm cần viền trang trí. Chu vi P = 4 × 10 = 40cm giúp xác định chiều dài đường viền.
- Thể thao và giải trí: Trong các môn thể thao hoặc trò chơi, chu vi hình vuông được dùng để xác định kích thước sân hoặc khu vực chơi.
Ví dụ: Một sân chơi cờ vua ngoài trời hình vuông có cạnh 3 m. Chu vi P = 4 × 3 = 12m giúp xác định chiều dài dây để đánh dấu ranh giới.
Qua những ví dụ thực tiễn trên, có thể thấy rằng cách tính chu vi hình vuông không chỉ là một kiến thức cơ bản trong Toán học mà còn là kỹ năng hữu ích trong nhiều lĩnh vực. Việc hiểu và áp dụng đúng công thức tính chu vi của hình vuông sẽ giúp chúng ta xử lý công việc chính xác, tiết kiệm thời gian và nâng cao hiệu quả trong học tập lẫn cuộc sống hàng ngày.
Trường Quốc tế Westlink với chương trình đào tạo chất lượng cao, đảm bảo học sinh được ứng dụng kiến thức vào thực tiễn. Không chỉ nằm lòng công thức tính toán, các bạn nhỏ theo học tại Westlink sẽ có cơ hội vận dụng công thức trong nhiều lĩnh vực khác nhau, đảm bảo tinh thần “vừa học vừa hành” cho trẻ.
THÔNG TIN LIÊN HỆ CỦA TRƯỜNG QUỐC TẾ WESTLINK
Địa chỉ: Đường Gia Vinh, Khu đô thị mới Tây Hồ Tây, Phường Xuân Tảo, Quận Bắc Từ Liêm, Hà Nội
Hotline: (+84) 865 777 900
Email: info@westlink.edu.vn
Kakao Talk: westlinkkr
Line ID: westlinkadmission


